2025.03.14 - [공부/강화학습] - [강화학습] Deep Q-Network ((DQN)) - 고급
[강화학습] Deep Q-Network ((DQN)) - 고급
2025.03.14 - [공부/강화학습] - [강화학습] Deep Q-Network ((DQN)) - 기본 [강화학습] Deep Q-Network ((DQN)) - 기본2025.03.10 - [공부/강화학습] - [강화 학습] Markov Decision Process ((MDP)) [강화 학습] Markov Decision Process
occident.tistory.com
1. Dueling DQN
기존 DQN과 다르게 $Q(s,a)$를 출력하는게 아니라 advantage $A(s,a)$와 state value $V(s)$를 출력한다.
1.1. Advantage Function
\[ A(s,a) = Q(s,a) - V(s)\]
\[ V(s) = \mathbb{E}[Q(s,a)]\]
즉, action 한 개의 value에 전체 action의 평균을 뺀 것과 같다. 양수가 나왔다는 것은 평균보다 좋은 행동이며, 음수는 평균보다도 안좋은 행동이라는 것을 알 수 있다.
1.2. Dueling DQN
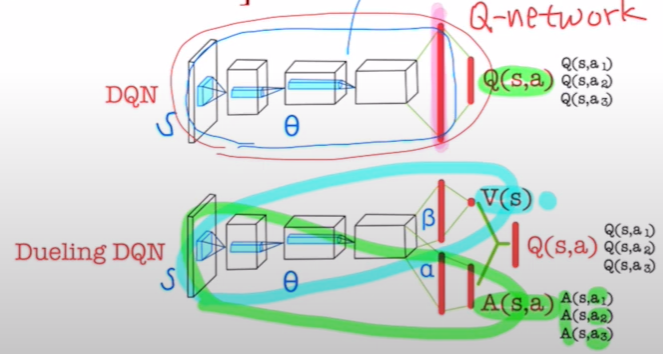
즉, Aggregator가 나오기 전까지는 동일한 네트워크를 사용하고 $V(s)$와 $A(s,a)$의 추정은 $\alpha, \beta$인 새로운 파라미터를 학습하여 추정한다. 이후, 합쳐서 각 action의 $Q$값을 추정한다.
기존의 DQN에서 가장 중요했던 것은 이 action을 하면 얼마나 좋을까?를 위주로 학습을 했지만, Dueling DQN에서는 state value ((즉, 나 지금 그냥 이 상태에 있는데, 나 지금 얼마나 좋은 상태인것 같아??))의 정보를 활용한다.
Dueling DQN의 장점은 agent의 action이 state에 큰 변화를 미치지 않았을 때, state value를 알 수 있기 때문에 더 유용하다.
Dueling DQN의 문제
identifiability Issue 발생 state value와 action value를 더하는 과정에서 발생하는 문제이다.
1.3. State Value를 estimation 할 수 있으면 생기는 장점

- 차가 멀리 있을 때
- State Value Saliency는 먼 곳을 하이라이트
- Advantage Value Saliency는 하이라이트가 없음
- 차가 가까이 있을 때
- State Value Saliency는 바로 앞의 차를 하이라이트
- Advantage Value Saliency 또한 바로 앞의 차를 하이라이
즉, 차가 멀리 있을 때처럼((어떤 액션을 취하는게 의미가 없는 상황))에서는 state value function이 더 좋을 수 있고
차가 가까이 있을 때는 advantage value가 더 좋을 수 있다.
Dueiling DQN은 매 step마다 action을 선택하는 환경보다 지금 그 상태가 얼마나 좋은 상태인지를 알아야하는 환경에서 더 우수한 성능을 보인다.
1.4. Identifiability issue
또한, $Q(s,a)=V(s)+A(s,a)$에서 $Q$를$V$와 $S$로 identifiable하게 분해할 수 없다는 문제가 있다.
예를 들어, 10 = 1+9 = 2+8 = 3+7 등의 많은 조합이 있기 때문이다.
$$
\left.Q^\pi(s, a)\right) {=}\left(V \pi(s)+A^\pi(s, a), V^\pi(s)=\mathbb{E}_{a \sim \pi(s)}\left[Q^\pi(s, a)\right] \text {, so } \mathbb{E}_{a \sim \pi(s)}\left[A^\pi(s, a)\right]=0 .\right.
$$
Advantage function의 expectation은 결국은 0에 수렴한다. ((무한 step을 진행하면 결국 state value와 action value는 같아진다.))
$$
\text { For a deterministic optimal policy, } a^*=\arg \max _{a^{\prime}} Q\left(s, a^{\prime}\right) \text {, and so } Q\left(s, a^*\right)=V(s) \text { and } A\left(s, a^*\right)=0 \text {. }
$$
Deterministic optimal policy에서는 최적 action value는 state value이기 때문에 optimal action에 대한 advantage function value는 0이다.
1.5. Identifiability issue's solution
$V(s),A(s,a)$ 둘 중 하나를 고정시키면 해결이 된다. 여기서는 Advantage function을 기준점으로 잡는다.
그 기준은!?
Best action을 선택했을 때 advantage value가 0이 되도록! <- 근거 있나? yes!
근거: 수식 1을 봤을 때, optimal policy를 선택하면 advantage value는 0이 되어야하고 동시에 action value와 state value가 같아진다.
$$
Q(s, a ; \theta, \alpha, \beta)=V(s ; \theta, \beta)+\left\lceil A(s, a ; \theta, \alpha)-\max _{a^{\prime}} A\left(s, a^{\prime} ; \theta, \alpha\right)\right] .
$$
Best action을 선택했을 때 advantage value가 0이 되도록하는 advantage function을 $A(s,a;\theta,\alpha)-\mathrm{max}A(s,a';\theta,\alpha)$로 잡아준다.
$$
a^*=\arg \max _{a^{\prime}} Q\left(s, a^{\prime} ; \theta, \alpha, \beta\right)=\arg \max _{a^{\prime}} A\left(s, a^{\prime} ; \theta, \alpha\right)
$$
Highest action value를 가지는 action이나, highest advantage value를 가지는 action은 동일한 action이다! 그 action을 $a^*$라고 할것이고
가장 높은 $\mathrm{max}A(s,a) = A(s,a^*)$와 동일한 것이다.
$$
A\left(s, a^*, \theta, \alpha\right)-\max _{a^{\prime}} A\left(s, a^{\prime} ; \theta, \alpha\right) .
$$
그러면, 가장 높은 action value를 가지게 하는 action을 통한 advantage function이 0이 되어 수식 1을 만족하게 된다. 수식 1을 만족하게 되면 가장 높은 action value를 가지게 하는 action을 통한 action value는 state value와 같아지게 되고 결국에는 unidentifiable 문제를 해결할 수 있게 된다.
$$
\max _{a^{\prime}} A\left(s, a^{\prime} ; \theta, \alpha \right)
$$
실제로 이 부분은 굉장히 variance가 크다. 따라서, 학습이 불안정해지기 때문에 실제로는 평균값을 취해주는게 더 성능이 좋다.
'ReinforcementLearning > 서적 요약' 카테고리의 다른 글
| [강화 학습] REINFORCE <Monte Carlo Policy Gradient> (0) | 2025.03.19 |
|---|---|
| [강화 학습] Policy Gradient Algorithm (1) | 2025.03.19 |
| [강화학습] Deep Q-Network <DQN> - 고급 (0) | 2025.03.14 |
| [강화학습] Deep Q-Network <DQN> - 기본 (0) | 2025.03.14 |
| [강화 학습] Markov Decision Process <MDP> (0) | 2025.03.10 |

